今天继续分享卷积神经网络,常常用深度学习这个术语来指训练神经网络的过程,有时它指的是特别大规模的神经网络训练。那么神经网络究竟是什么呢?我们先来看一些直观的基础知识。
让我们从一个房价预测的例子开始讲起。
假设你有一个数据集,它包含了六栋房子的信息。所以,你知道房屋的面积是多少平方英尺或者平方米,并且知道房屋价格。这时,你想要拟合一个根据房屋面积预测房价的函数。
如果你对线性回归很熟悉,你可能会说:“好吧,让我们用这些数据拟合一条直线。”于是你可能会得到这样一条直线。
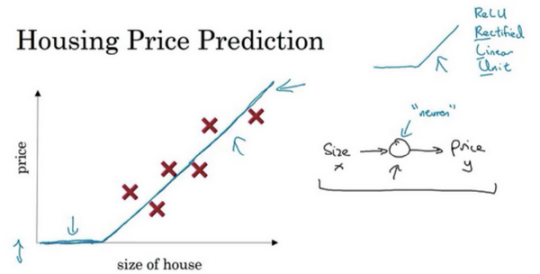
但有点奇怪的是,我们知道价格永远不会是负数的。因此,为了替代一条可能会让价格为负的直线,我们把直线弯曲一点,让它最终在零结束。这条粗的蓝线最终就是我们要的函数,用于根据房屋面积预测价格。有部分是零,而直线的部分拟合的很好。你也许认为这个函数只拟合房屋价格。
作为一个神经网络,这几乎可能是最简单的神经网络。我们把房屋的面积作为神经网络的输入(我们称之为$x$),通过一个节点(一个小圆圈),最终输出了价格(我们用$y$表示)。其实这个小圆圈就是一个单独的神经元。接着网络实现了左边这个函数的功能。
在有关神经网络的文献中,经常能看得到这个函数:从趋近于零开始,然后变成一条直线。这个函数被称作ReLU激活函数,它的全称是Rectified Linear Unit。rectify(修正)可以理解成$max(0,x)$,这也是你得到一个这种形状的函数的原因。
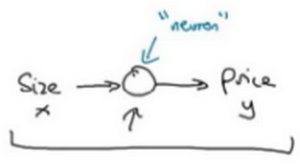
你现在不用担心不理解ReLU函数,你将会在这门课的后面再次看到它。
如果这是一个单神经元网络,不管规模大小,它正是通过把这些单个神经元叠加在一起来形成。如果把这些神经元想象成单独的乐高积木,就可以通过搭积木来完成一个更大的神经网络。
让我们来看一个例子,我们不仅仅用房屋的面积来预测它的价格,现在你有了一些有关房屋的其它特征,比如卧室的数量,或许有一个很重要的因素,一家人的数量也会影响房屋价格,这个房屋能住下一家人或者是四五个人的家庭吗?而这确实是基于房屋大小,以及真正决定一栋房子是否能适合你们家庭人数的卧室数。
换个话题,你可能知道邮政编码或许能作为一个特征,告诉你步行化程度。比如这附近是不是高度步行化,你是否能步行去杂货店或者是学校,以及你是否需要驾驶汽车。有些人喜欢居住在以步行为主的区域,另外根据邮政编码还和富裕程度相关(在美国是这样的)。但在其它国家也可能体现出附近学校的水平有多好。
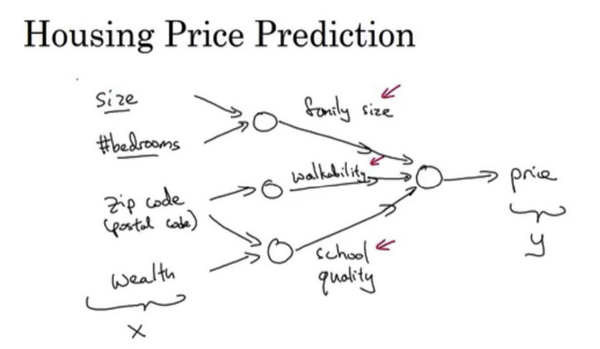
在图上每一个画的小圆圈都可以是ReLU的一部分,也就是指修正线性单元,或者其它稍微非线性的函数。基于房屋面积和卧室数量,可以估算家庭人口,基于邮编,可以估测步行化程度或者学校的质量。最后你可能会这样想,这些决定人们乐意花费多少钱。
对于一个房子来说,这些都是与它息息相关的事情。在这个情景里,家庭人口、步行化程度以及学校的质量都能帮助你预测房屋的价格。以此为例,$x$ 是所有的这四个输入,$y$ 是你尝试预测的价格,把这些单个的神经元叠加在一起,我们就有了一个稍微大一点的神经网络。这显示了神经网络的神奇之处,虽然我已经描述了一个神经网络,它可以需要你得到房屋面积、步行化程度和学校的质量,或者其它影响价格的因素。
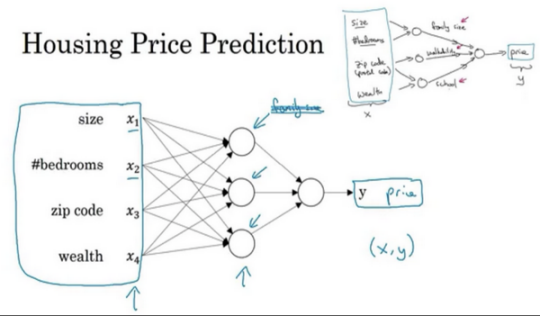
神经网络的一部分神奇之处在于,当你实现它之后,你要做的只是输入$x$,就能得到输出$y$。因为它可以自己计算你训练集中样本的数目以及所有的中间过程。所以,实际上要做的就是:这里有四个输入的神经网络,这输入的特征可能是房屋的大小、卧室的数量、邮政编码和区域的富裕程度。给出这些输入的特征之后,神经网络的工作就是预测对应的价格。同时也注意到这些被叫做隐藏单元圆圈,在一个神经网络中,它们每个都从输入的四个特征获得自身输入,比如说,第一个结点代表家庭人口,而家庭人口仅仅取决于$x_1$和$x_2$特征,换句话说,在神经网络中,你决定在这个结点中想要得到什么,然后用所有的四个输入来计算想要得到的。因此,我们说输入层和中间层被紧密的连接起来了。
值得注意的是神经网络给予了足够多的关于$x$和$y$的数据,给予了足够的训练样本有关$x$和$y$。神经网络非常擅长计算从$x$到$y$的精准映射函数。
这就是一个基础的神经网络。你可能发现你自己的神经网络在监督学习的环境下是如此的有效和强大,也就是说你只要尝试输入一个$x$,即可把它映射成$y$,就好像我们在刚才房价预测的例子中看到的效果。
内容推荐:机器学习与网络安全
地址:https://www.aqniukt.com/course/4868/tasks



